二項モデル自体についてはわかりやすい解説が多数紹介されていますのでここでは省略します。
一方、実際に使える実装方法はなかなか見当たりませんので、ここでは、1年間を252分割して(1年間を252取引日と近似)日次で株価変動をシミュレーションする想定でも無理なく動くのコード例を示します。
プレーンバニラを二項モデルで評価するコード
library(Rcpp)
cppFunction('
double BM_plain(double S0, double K, int end_step, int ex_start, double u, double d, double df, double p) {
NumericMatrix c_step((end_step+1), 7);
NumericMatrix n_step((end_step+1), 7);
for(int step = end_step; step >= 0; step--) {
for(int node_no = 0; node_no <= step; node_no++) {
double S = S0 * pow(u, (step - node_no)) * pow(d, node_no);
double hd_v = 0; // 保有価値
double ex_v = 0; // 行使価値
double op_v = 0; // オプション価値
if(step == end_step) {
// 満期時のノードの場合
hd_v = 0;
ex_v = S - K;
op_v = (ex_v > hd_v) ? ex_v : hd_v;
c_step(node_no, 6) = (S > K) ? 1 : 0;
} else if (step == 0) {
// t=0(評価基準日)のノードの場合
hd_v = df * (p*n_step(node_no, 5) + (1-p)*n_step(node_no+1, 5));
ex_v = 0;
op_v = (ex_v > hd_v) ? ex_v : hd_v;
op_v = hd_v;
} else {
// 0<t<Tのノードの場合
hd_v = df * (p*n_step(node_no, 5) + (1-p)*n_step(node_no+1, 5));
if(step < ex_start) {
// 待機期間中の場合
ex_v = 0;
op_v = hd_v;
c_step(node_no, 6) = 0;
} else {
// 行使可能期間中の場合
ex_v = S - K;
op_v = (ex_v > hd_v) ? ex_v : hd_v;
c_step(node_no, 6) = (ex_v > hd_v) ? 1 : 0;
}
}
c_step(node_no, 0) = step;
c_step(node_no, 1) = node_no;
c_step(node_no, 2) = S;
c_step(node_no, 3) = hd_v;
c_step(node_no, 4) = ex_v;
c_step(node_no, 5) = op_v;
}
// ファイルの出力
// Function f("write.csv");
// String file_name = "testcase/check"; file_name += step; file_name += ".csv";
// f(c_step(Range(0, step) , _ ), Named("file")=file_name);
n_step = clone(c_step);
}
return(c_step(0, 5));
}
')
処理の流れ
コードは株価など基本的なパラメータの他、二項モデルの上昇幅\( u \)、下落幅\( d \)、割引係数\( df \)それから(リスク中立)上昇確率 \( p \)をインプットとして受け取ります。これらについては下の「使い方」をご参照ください。
end_stepは分割数です。同時に、オプションの満期時点という意味も持ちます。まずはend_step時点(オプションの満期時点)から開始して、時点0(評価基準日)までバックワード計算を行っていきます。
end_step時点の情報に基づきcurrent_stepなるテーブルを作っていきます。current_stepは下の7列からなります。
- ステップ数(満期時点なのでend_step)
- ノード番号(上から順に0,1,2,・・・)
- 株価(ノード番号0が満期時点でとり得る最大の株価(つまり満期時点までの各ステップで1度も株価が下降しなかった場合)
- オプションを行使せず保持する価値(満期時点なので0)(コード19行目)
- オプションを行使する場合の価値(コード20行目)
- オプションの価値(4.と5.の価値の大きい方(正確には小さくない方))(コード21行目)
- そのノードで行使されるなら1, 保持するなら0、とするフラグ
current_stepが出来上がったところで、これをnext_stepなるテーブルにコピー(値コピー)します。
次にステップ数を一つ下げて(つまり、満期時点から1ステップ下がった時点で)、同様にcurrent_stepを作っていきます。
- ステップ数(end_step-1)
- ノード番号(上から順に0,1,2,・・・)
- 株価(ノード番号0がend_step – 1でとり得る最大の株価(つまり満期時点までの各ステップで1度も株価が下降しなかった場合)
- オプションを行使せず保持する価値(next_step上の(つまり満期時点の)情報を参照して計算)(コード33行目)
- 行使可能あればオプションを行使する場合の価値(コード42行目)、まだ行使できないのであれば0(コード38, 43行目)
- オプションの価値(4.と5.の価値の大きい方(正確には小さくない方))(コード37行目)
- そのノードで行使されるなら1, 保持するなら0、とするフラグ
end_step-1時点のcurrent_stepを作るために、next_stepに保存しておいたend_step時点の情報を参照しているわけです。
次にステップ数をもう一つ下げて(満期時点から2ステップ下がった時点で)同様にcurrent_stepを作ります。その際、end_step-1時点の情報を参照するため、今作ったcurrent_step(end_step-1時点の情報)をnext_stepに上書き(値コピー)します。つまり、next_stepに保存されているend_step-1の情報を使用して、end_step-2時点におけるcurrent_stepを作ります。
これをステップ1まで繰り返します。
最後に評価基準日時点(ステップ0)のcurrent_stepを作ります。
- ステップ数(0)
- ノード番号(0のみ)
- 株価(S0)
- オプションを行使せず保持する価値(next_step上の情報を参照して計算)(コード26行目)
- オプションを行使する場合の価値、発行時点では行使不可として0(コード27行目)
- オプションの価値(4.の価値)(コード28行目)
- そのノードで行使されるなら1, 保持するなら0、とするフラグ
このcurrent_stepの6列目(列番号5)が、求めたいオプションの評価額です。
計算プロセスの出力
57行目から59行目のコメントアウト(// でコメントアウトです。)している部分は、各current_stepをCSVファイルに出力する処理です。今述べたプロセスを確認する目的で、また、自分で行った評価の正しさの検証のため、必要に応じてコメントアウトを解除して活用してください。
実行上の注意点
実行上の注意点が3つあります。
- ファイルの出力は作業ファイルの下に「testcase」というフォルダがある想定です(58行目 file_name = “testcase/check”・・・)。あらかじめ作成しておいてください。52行目のtestcaseを変更して他の名前のフォルダとしても問題ありません(注)。
- すべてのcurrent_stepが出力されます。上に記載の設定のまま出力すると、\( 10 \times 252=2520 \)枚のCSVファイルが出力されます。処理に時間がかかるうえ、そんなにたくさんのファイルを確認することはできないと思います。確認用にはend_step=10とか=20で十分だと思います。
- 処理に変更を加える都度(1.のコメントアウト・除外を行う都度)、コンパイルしなおす(cppFunction(‘・・・’)を実行しなおす)必要があります。
(注)フォルダがなければ作成する、あればその中身を空っぽにする、という処理を57行目の上に加えると便利です。(評価と関連しないので解説はしません。)
実装上の注意
他の言語で実装する場合、current_stepからnext_stepへのコピーは「参照コピー/シャローコピー」でなく「値コピー/ディープコピー」とする点にご留意ください。(61行目のclone()関数はRcppのディープコピーです。)よりよい実装があればぜひご教示ください。
使い方
1年間を252取引日と想定し、1年を252分割する(\( delta \))ものとなっています。下の例では満期\( Y \)を10年と置いたうえで分割数end_stepを\( Y×252 = 2520 \)とし、その分割数に応じて年率である\( \sigma, r, q \)を変換しています。
月単位での分割とするのであればコード中\( delta \)を12とします。1日をさらに10分割するのであれば、\( delta \)を2520とします。
80行目で行使期間開始時期をインプットしています。コードでは開始時期=Y(=満期)としているので、満期時点でのみ行使可能な想定での評価となっています(ブラック・ショールズ式による評価額と(ほぼ)一致します。)。
待機期間がなく発行時から即時行使可能となる場合は行使期間開始時期を\( 0 \)とします。
また、発行後2年後から行使可能とする場合には、行使期間開始時期を\( 2 \times 252 \)とします。
23行目から26行目で二項モデルの上昇幅\( u \)、下落幅\( d \)、割引係数\( df \)および(リスク中立)上昇確率 \( p \)を算出しています。これらの23行目から26行目のように計算すると「ブラック・ショールズ・モデルと同様の仮定を置く」ことになります。
{
S0 <- 1000 # 株価
K <- 1000 # 行使価格
sgm <- 0.5 # ボラティリティ(年率)
r <- 2 / 100 # 無リスク金利(年率)
q <- 50 # 配当金額(年額)
Y <- 10 # 満期(年)
t1 <- 10 # 行使可能期間の開始時期(年)
delta <- 252 # 分割数(1年を何分割するか)
}
# インプットの変換
{
q <- q / S0
end_step <- Y * delta # 満期
ex_start <- t1 * delta # 行使可能期間開始時期
sgm <- sgm * sqrt(Y) / sqrt(end_step)
r <- ( (1+r)^Y )^(1/end_step) - 1
q <- ( (1+q)^Y )^(1/end_step) - 1
u <- exp(sgm)
d <- 1/u
df <- exp(-r)
p <- (exp(r-q) - d) / (u - d)
}
BM_plain(S0, K, end_step, ex_start, u, d, df, p)
行使境界の可視化
testcase フォルダに出力されるcheck〇.csvファイルで、一番右の列が「1」となっている箇所で行使が起こっているので、これを辿っていけば行使境界を容易に可視化できます。プレーンバニラの場合、配当がなければ早期行使は起こらないことも確認できます。
参考までに、配当がある場合の行使境界を図示します(\( S(0) = K = 1000 \)、配当年額50)。
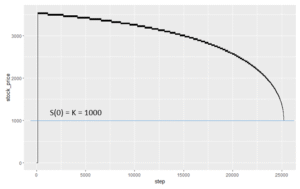
横軸はstep 数です(右端が満期)。縦軸は株価でカーブより上の領域では早期行使が有利になっています。
株価が離散的なためカーブが太さを持って見えますが、連続的であったとすると、この太みの真ん中を通るような曲線となろうかと思います。t = 0 近辺では株価がまだ十分に上方に広がっておらず、早期行使は起こっていません(行使境界の値をゼロとしています)。
配当がない場合であっても、バリアオプション等株価条件によっては早期行使が発生します。

